Annex 2

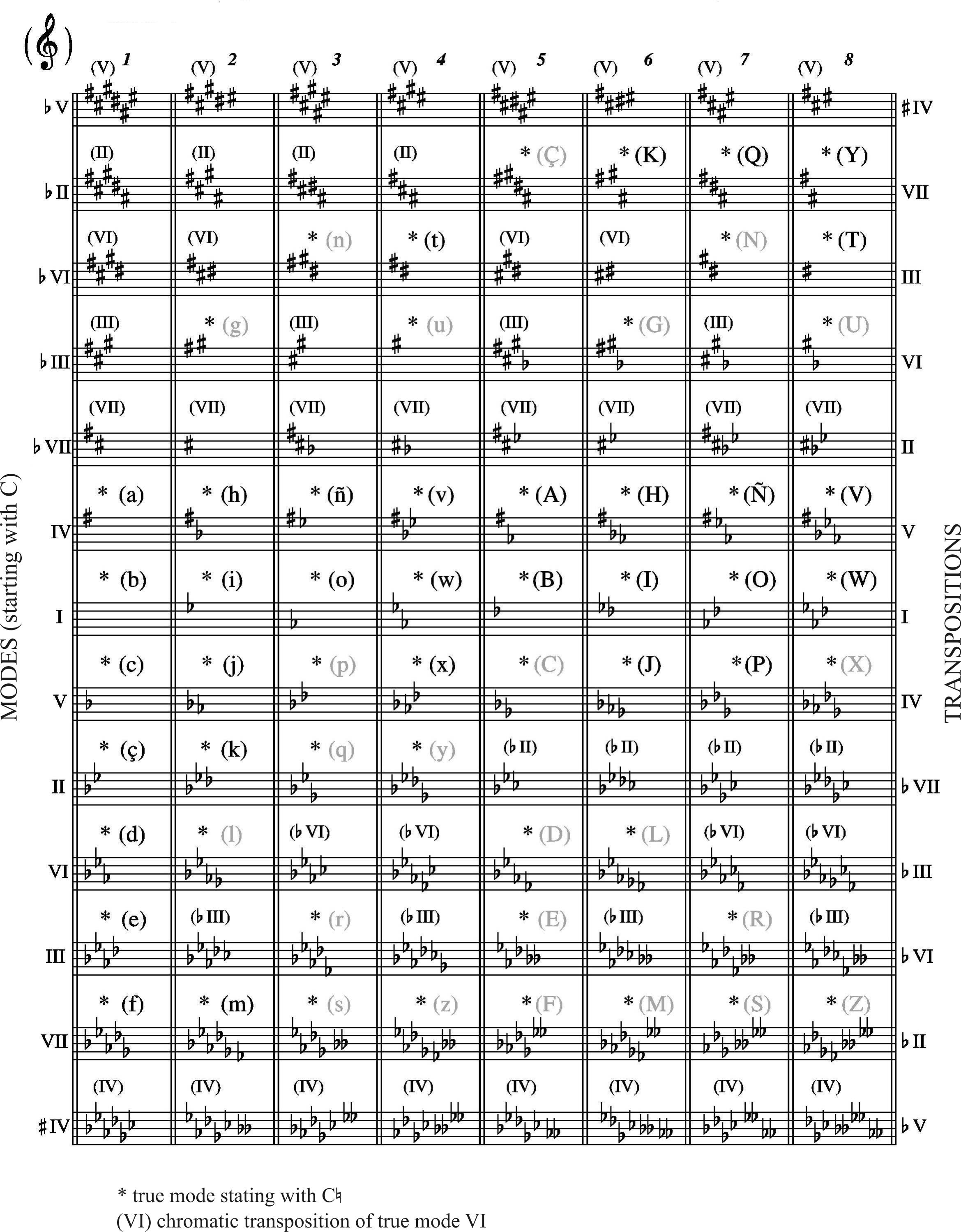
9. Modes of the first eight 7-note scale classes

The first eight 7-note scale classes have in common that the notes of their modes can be written as different chromatic alterations of the major mode diatonic scale. In fact, this could be done for the majority of 7-note scale classes (forcing the enharmony to the extreme) but, except for some cases, only with the first eight scale classes can this be done without adversely affecting the harmonic significance of the notes.

For example, the C-D-F-G-A¬-B¬-B} scale (chord/scale class #19) could be written as a chromatism of the diatonic scale as follows: C-D-E{-Fx-G{-A{-B or, another example, C-D¬-D}-F-G-A-B (chord/scale class #11) could be as well written as C-D¬-E¬¬-F-G-A-B. But in both cases there could be an inaccuracy regarding the harmonic meaning of the notes because both scales contain the convergent structure (GBDF) which is the one that establishes the tonic C. So, in the first case E{ and Fx should be F and G and in the second case E¬¬ has to be D} (Figure 79).

Fig.79

The fact that the first eight scale classes (and their modes and transpositions), could be written as major diatonic scale chromaticisms is very useful because there is no need to put notes to show the scale classes modes, it is enough to indicate the key signature on the stave. This saves space and allows to express the harmonical relationships between all the modes of the eight scale classes in a clear way.

The meaning of the Modes Table 6 in this appendix is as follows:

Each column belongs to a scale class and each row to a mode. Even if there are 13 rows, there is only 7 authentically different modes for each column (those marked with *), the rest are their chromatical transpositions (all those having C{ or C¬ on the key signature —the roman number in parentheses shows the original mode—).

On the central row, belonging to I, there are the representatives of each scale class as shown in the Chord/scale class tables. These are the most stable modes in the sense that they start with the most tonicizated note. The left roman numbers

The modes that have the perfect fifth from the initial note can also be studied and classified from the point of view of the two tetrachords:

Fig. 79bis

To know a mode, it is enough to form a heptatonic scale, starting by C and put the accidentals indicated on the key signature. For example, 7th. column, row 6 is the mode of the degree IV from scale class #7 and has as a key signature F{, E¬ and A¬. The scale C-D-Eb-F{-G-A¬-B will represent the structure of this mode (named gipsy or hungarian mode). The transpositions of this mode to another tone could be easily known looking at the degrees that appear on the right hand side of the table, bearing in mind that each row represents a 5th. interval. Like that, if one wants to transpose this mode a rising major 2nd. it will be sufficient to look two rows higher (or find the degree V+M2=VI —on the right—) and see the key signature C{, G{ and B¬. But now, instead of starting by C it is necessary to start obviously by D. So the scale D-E-F-G{-A-B¬-C{ is the same mode applied to D (C+M2) (See also Figure 74 on Annex 1).

The division of the octave into seven sounds or intervals has been one of the most common in all musical cultures. Using only the modes of the first eight 7-note scale classes we obtain a wide range of expressions and musical colours. The names of some of these modes are listed on Table 7 (assuming the needed tune adjustments in each case) according to the musical theories of different countries.¹ Other known modes, particularly the Hindus, don't appear because they are in other chord/scale classes. We also indicate in this table its separation in tetrachords according to figure 79bis.

¹ As far as the ecclesiastical modes after the Oktoechos are concerned, the names appearing in the Dodecachordon (1547) of Glareanus have been used, grouped according to the criterion of finalis=tonic (1st degree). The same criterion has been followed in Iranian-Arabic music over the 12 dastgah-ha. Hindu modes have been extracted from the 72 malakartas of the (south) carnatic theory according to Venkatamakhi and the 10 thate of the Hindu (north) theory according to Bhathhande. All this information has been collected from The New Grove Dictionary of Music (London), Encyclopedie de la Musique (Paris), Danielou (1943) and sporadically from other sources. There are small divergences, which are manifested with a question mark.

1-I    (b)   MM     Modo mayor, Lidio griego, Jónico (plagal hipojónico), Dhira-shankarâbharana, Bilaval, segah, chin tiao

1-V   (c)   Mm      Modo de Sol, Hipofrigio griego, Tetrardus, Mixolidio (plagal hipomixolidio), Hari-kâmbhoji, Matsaríkrta, Khammaj(?), bayat-e tork (mahur?), rast, shang tiao

1-II    (ç)* mm      Modo de Re, Frigio griego, Protus, Dórico (plagal hipodórico), ruso menor, Kharahara priya, Sudda Sadja, Kâfi(?), hyojo (ritsu), yü tiao

1-VI  (d)'  mn       Modo menor natural o descendente, Hipodórico griego, Eolio (plagal hipoeolio), Nata-bhairavi, Asâvari, Isfahân (afshari?), chüeh tao

1-III   (e)   nn       Modo de Mi, Dórico griego, Deuterus, Frigio (plagal hipofrigio), Hanumat-todi, Bhairavi, shur (nava), zokuso, pien kung tiao

1-VII  (f)              Modo de Si, Mixolidio griego, Locrio, Shahnaz (dashti?), pien chih tiao

2-IV   (h)   M⁺m   Modo de los armónicos II (Scriabin, Albrecht, Szymanowski), Modo de Podhale (Polonia), Acústica (Bartók), Vâchaspati

2-I      (i)    mM    Menor ascendente, "Hawaiano", Gauri-manohari

2-V    (j)*  Mn      Mayor-menor, Châru-késhi

2-II    (k)'  nm       Nâtaka-priya

2-VII (m)              Super Locrio

3-IV   (ñ)   m⁺M    Dharmavati

3-V    (p)   Nm       Menor armónico inverso, Chakravâka

3-I      (o)   MN       Mayor armónico, Modo de Hauptmann, Saransángi

4-bVI  (t)                Kosala

4-IV    (v)    m⁺m    Dórico ucraniano, Haimavati, Homayun

4-I      (w)    mN     Menor armónico, Gitano español, Andaluz, Kiravâni, bayat-e esfahan

4-V    (x)      Nn      Frigio dominante, Vakulâbharana, Shad Araban, Alhijaz

4-VII  (z)                 Ultra locrio

5-IV   (A)    M⁺N    Latângi

5-I     (B)     NM     Sûrva-kânta

5-III  (E)                 Senâpati

5-VI  (D)                Sabach (Grecia)

6-IV  (H)    M⁺n     Modo de los armónicos I, Rishabha-priya

6-I     (I)*   nM       Napolitano mayor, Círculo cerrado de cuartas según J.Darias, Kokila-priya

6-V   (J)'                 Locrio mayor

6-bII (K)                Escala de tonos con sensible

6-VII (M)               Escala de tonos con sensible descendente

7-IV (Ñ)   m⁺N      Gitano menor, Húngaro menor, Doble armónico menor, Niavent (Grecia) Simhendra-madhyama

7-I    (O)* NN      Doble armónico, Bizantino, Gitano mayor, Mâyâ-malava-gaula, Bhairav, Tchahârgah

7-V   (P)'                Modo de Wollet, Oriental, Tsinganikos (Grecia), Raga Ahira-Lalita

7-bII (Q)                Râsika priya

8-bVI (T)               Shûlini

8-IV  (V)   m⁺n      Modo gitano húngaro (?), Shanmukha priya

8-I    (W)    nN       Napolitano menor, Dhenukâ, Todi (?)

8-bII (Y)                Chitrâmbari

Redonda: Modos occidentales
Cursiva: Modos indios/hindús
Negrita: Modos irano-árabes
Negrita-cursiva: Modos japoneses o chinos
( )*: Modo simétrico respecto G (incluyendo la 8ª de C)
( )': Modo simétrico respecto F

Annex 3