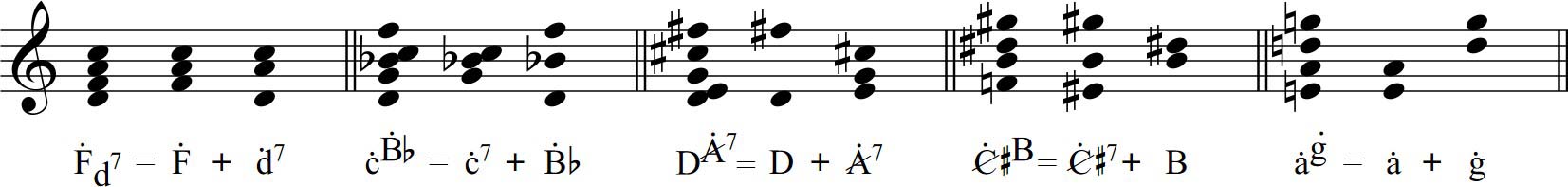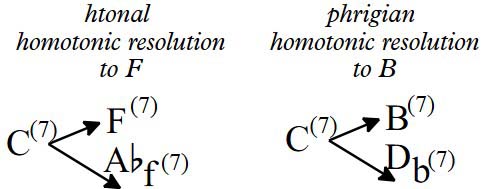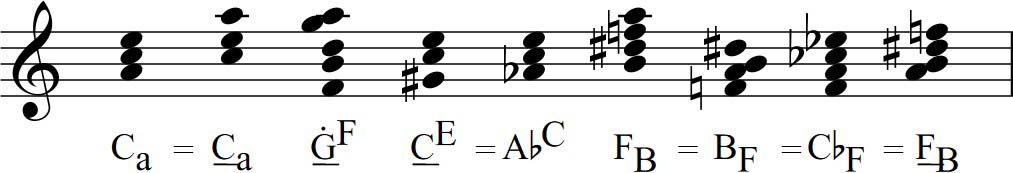3. Functional study of chords

I use the term chord in the title, but when I speak of chords I mean also arpeggios and in general the set of harmoniously significant notes that occur in a given time neighbourhood, although the graphical representation is in chord form.

We have already seen in these first two chapters which are the main intervals that cause harmonic tension and in 1.6 and 1.7 we have introduced the way to encode the chords so that this symbology gives us information about these tensions (the tensions of M3 and tritone). Next we will establish the eight large families of chords that can be constructed considering their internal harmonic tensions, determined mainly by the interval formed by their main functional fundamentals.

3.1 Classification of chords according to their harmonic tensions. The fundamental symbology

Regardless of their consonance or dissonance (sonance) we could make a classification of the chords according to their harmonic function represented by their functional fundamentals. I call fundamental symbology the system used to represent the fundamentals of chords. Let's summarize how it works:

First recall here figures 7 and 8. A capital letter means that we have a tension of M3 in the chord and a capital letter with a 7 or a crossed one means that in the chord there is a tritone tension (in the second case with a virtual fundamental). We call functional fundamentals to the fundamentals in capital letter since they represent a chord with "quasi-fifth" tension. The combinations of notes corresponding to the first seven harmonics are thus represented by a single letter (representing the fundamental), with different symbols depending on the combination of these notes (figure 7), although in everyday practice, for the most common chords, we do not usually distinguish whether the fundamental has the fifth or not.

Fig. 7

Fig. 8

If we have two fundamentals, we put in the upper part (superscript) the fundamental that is harmonic of the other. If they are on the same tonal axis (see 4.5), we put in the lower part (subscript) the lower minor 3rd or the tritone. In figure 8 we have some examples.

That is, if the symbol has the form X^Y means that Y is a fundamental a fifth, a major third or a minor seventh from the fundamental X. If the symbol has the form X_Z (X, Y and Z may be in uppercase or lowercase) means that Z is a fundamental a lower minor third or a tritone with respect to X. If the two fundamentals are separated by a semitone, we usually put it in the form X^Y, where Y is the major seventh, although sometimes we also put the minor second above (usually when there is a Z below, for more details see annex 1).

When the fundamental has its minor seventh in the chord, we place a 7 above (except when Y is precisely the minor seventh of X). When we have two fundamentals, we put a dot on those that have their fifth in the chord, with two exceptions: when Y is precisely the fifth of X (we do not put a point on the X) and when Z is the minor third of an uppercase X (we do not add a point to Z because it is already implicit —X in uppercase means that it has the M3, which is the fifth of Z—, this saves us work by symbolizing the minor chords). As you look in this chapter at the examples of the different kinds of chords it will be easier to understand how the fundamental symbology works, which I think is quite simple.

In any case what is really important is to know the fundamentals of the chords. The way they are placed is secondary.

Fig. 23

This fundamental symbology informs us that these functional fundamentals (as we have seen in 1.2 and 1.7.2) tend to «resolve» in other fundamentals that are a lower fifth/upper fourth (htonal resolution) or a lower minor second/upper major seventh (Phrygian resolution) (figure 23), aside the secondary resolutions that will

be seen in chapter 4. I use the term "resolution" in a broad sense, when I use it, I mean in general a progression or succession in which the passage to the next chord is harmonically and locally relaxed, either as the end of a musical section or not. We will devote the entire chapter 6 to place examples of different combinations of these local homotonic relaxions/resolutions with different types of chords.

3.1.1 Major chord family

They are chords of genre C or C^G.

They are made up of notes corresponding to the harmonics 5f and 3f of C and the harmonics 5f and 3f of the fifth of C.

We have represented some of them (ordered by consonance) in figure 24.

Fig. 24

A subdivision can be made between those with a single fundamental (the major triad) —a single tension of M3— and those with two fundamentals —two tension of M3— at a distance of fifth.

They are tonally stable chords and can be used as endings of compositions, preferably with the fundamental on the bass. His notes form combinations of 2f, 3f and 5f (they have some or all of the following notes corresponding to the harmonics: 2f [C], 3f [G], 5f [E], 3f of 3f [D], 5f of 3f [B]). In case of C^G, the tension GB towards C is «satisfied» if in the bass we hear C, although it can also resolve in another chord based on C. The C (as fundamental) can be kept stable or continue a progression in chords based on F or B (if we want it relaxed). Also secondarily we have homotonic relaxion in chords based on D and E (as will be seen in 4.1 and 4.2).

The different chords of this family may have a very different sonance but all have a similar harmonic function and in this chapter we are classifying the chords by their harmonic function, not by their consonance or dissonance.

The chords C^~g (CEGD), C^~e (CEB), ~d^C (CEDA) and ~ d^~C (CEGDA) can also be considered within the major chord family (of C) since the fifths ~g, ~e y ~d do not change the global function of the family. They are chords that could also substitute relaxed tonic chords (preferably placing C on the bass). In fact, C^~e chord could also be coded C^\G, since the notes C, E, B cause the G to be virtually heard as harmonic (fifth) of C.

In general, adding a lowercase does not alter the chord function too much as long as new functional fundamentals are not created, that is, new intervals of M3 or tritone between the notes of the chord. In this case we would have a new functional fundamental with new tension.

Located at the border of the functional change, the chord formed by three major triads at a fifth distance (CEGBDF{A), with C on the bass, although it has three functional fundamentals (C, G and D), we could also consider it as belonging to this family.

For more information on the resolutions, successions or progressions of this chord family see also 6.1 and 6.2.3.

3.1.2 Minor chord family

They are chords of genre C_a or C^G_a.

That is, they have the functional fundamentals of major chord family with a lower third of the main functional fundamental, which may be in the bass or not.

We have represented some of them (ordered by consonance) in figure 25. The C, as a capital letter, implies that it has the note E, so A always has its fifth E, so it is not necessary to put a point on a (C_ã) nor to put the µ if its seventh minor G already appears in the code.

Fig. 25

For more details on the minor triad, see 2.7.

Minor chord family can also be used to finalize a composition or a musical section.

As in the case of major chord family, a subdivision can be made between those having a single tension of M3 and those having two M3 at a distance from P5 (and also, of course, distinguishing between the minor triad and the others).

They have A (a) as weak fundamental due to the convergent structure AE(G) contained (harmonics 5f and 7f), but, as we have seen, functionally the main fundamental, as representative of the function of the chord, is C.

The resolutions or relaxed progressions are similar to those of the major chords. In fact we could have put them in a single family, but in this case, the different characteristic sonance of the major and minor chords has made me choose to separate

them into two families since, as we say, functionally could have been included in a single one.

For more information on links to these chords see also 6.1.

3.1.3 Dominant chords (unitonal)

They are the chords that contain a single 7M3 structure (in real or virtual form) and therefore they form (by themselves) a very strong tonal vector. Hence the name of dominant, by its cadential force towards chords based on the tonic established by 7M3 (F in the examples).

We have placed in other families chords that contain more than one 7M3 structure, such as, for example, symmetric dominant chords (3.1.5); however, they must also be considered dominant chords, what happens is that they are dominant of two or more tonics. In fact the unitonal dominant chords and the symmetric dominant ones have many similarities and could also have been put into a single large family of dominant chords.

They are chords of genre C⁷ or C^B¬ (and Cµ_a or C^B¬_a).

We have represented some of them in figure 26.

Fig. 26

It is also possible to establish a subdivision between those who have a single functional fundamental and those who have two, but all have a clear cadential force towards F as they contain the subdominant, the dominant (real or virtual) and the leading-tone of the tonality (the structure 7M3). Those with two functional fundamentals these are precisely (as fundamentals) the dominant (C) and subdominant (B¬) of the theoretical tonic (F).

We have placed in this family also the dominant seventh chord plus a minor ninth. This chord, from another point of view, is a diminished seventh chord (which has four virtual fundamentals at a distance of m3) in which one of the four possible virtual fundamentals becomes real, therefore dominates over the others (although we have to take into account the small tension that also create the other virtual ones). This chord will be symbolized with 9, so when we see a 9, just like when we see a 7, it refers to the interval of minor 9th (in jazz normally the symbol ¬9 is used). It is important not to confuse it with the dominant 9th chord (with the major 9th).

This chord is coded C^B¬ (since it includes the major thirds CE and B¬D). 7 and 9 are the only numbers we use in the fundamental symbology and always refer to the minor 7th and minor 9th intervals.

The diminished seventh chord, if the tonality is well established, can also be placed in this family and symbolized as a ninth chord we have seen before but with virtual fundamental, wich plays the dominant function (\~C⁷⁹); but only in the case that there are no enharmonic tonal confusions since it structurally does not have a single fundamental and therefore is not strictly unitonal dominant. When the tonality is not defined this chord has four symmetrical fundamentals in competition with each other and therefore we have placed it also in the family of the symmetric dominant chords (3.1.5). This chord has one foot in each of the two families.

For more information on the unitonal dominant chords see 6.2.2.

3.1.4 Augmented chords

They are chords of genre C^E (and C_a^E).

They have the fifth of the functional fundamentals augmented (or the m6 from another point of view). Some examples are shown in figure 27.

Fig. 27

These chords have always a third hidden fundamental since there is another M3 (enharmonic): A¬(G{)-C. It is not necessary to put this third fundamental in the symbology, unless it is in the bass (then we would write A¬^C instead of C^E), but we have to consider its existence.

Like the diminished seventh chord, the three-note version of the family is a chord dividing the octave into equal parts.

For more information on links to this chord family see 6.2.4.

So far we have seen families of chords with one or two functional fundamentals whose intervals (between the two fundamental) are of P5, M3 or m7, that is, correspond to the harmonic intervals 3f, 5f and 7f from the main fundamental.

The two families that will be discussed below also have two functional fundamentals, but separated by m3 or tritone intervals. That is, they are on the same

tonal axis (see 4.5). To distinguish them from the other families we will put the second fundamental in the lower part (instead of superscript) (also for maintaining the coherence with the minor chords where we have written the lower minor 3rd in lowercase as subscript of the functional fundamental).

3.1.5 Symmetric dominant chords

They are chords of genre C_G¬ o C_F{.

They are chords that have two tensions of M3 (and also two of 7M3). The fundamentals are separated by a tritone interval.

We have represented some of them in figure 28.

Fig. 28

The two fundamentals of these chords divide the octave into two equal parts. That is to say, we have two M3 in symmetry and the order of the two fundamentals, in the symbology, could be the other way around. This distance of tritone automatically implies that the two fundamental also have their minor 7th (enharmonized or not). Which means that the two fundamentals have the 7M3 structure, but in competition between them in the sense that the two tonal vectors are in the opposite direction in the circle of fifths. This, and the fact that it is not a very dissonant chord, gives it a very characteristic sonance. Therefore, they are chords with (double) dominant function. They could have been placed in the dominant family, but we preferred to separate them due to the difference between the functional fundamentals.

We have also placed here the diminished seventh chord, since if we take its virtual fundamentals, it could also be considered belonging to this family, but we would have to add two more virtual fundamentals, all four separated by minor thirds. As we said in 3.1.3, when the diminished seventh chord is inserted in a clear tonal neighbourhood and there are no possible harmonic confusions —for example, the diminished 7th chord on the 7th degree (leading-tone) of the minor mode—, then we will symbolize it as \~G⁷⁹ (in C minor) and it will be a chord that will be between this family and the unitonal dominant chord family, although structurally it still has four symmetric virtual fundamentals. Of the four we usually write at most two, the most significant ones according to the harmonic context in which they are laid (separated by a tritone or a m3).

When the m7 of C (B¬) is enharmonized as M3 of the other fundamental F{ (A{) we find the much used french augmented sixth chord (CEF{A{).

For more information on these types of chords and their links see 6.2.1.

3.1.6 Major-minor chords

They are chords of genre C_A.

They are chords in which a fundamental forms, simultaneously, a major triad and a minor triad (apart other possible added notes). Automatically, a second functional fundamental (a minor 3^rd up) appears. There is a "collision" of m2 between its major 3^rd and its minor 3^rd, which is the other fundamental. They are rather dissonant chords.

We have represented some of them in figure 29.

If we include the fifth of C, automatically A acquires its m7 and therefore we obtain the 7M3 structure (AC{G) and it gain a dominant flavor (tonal vector towards D) (this chord is pretty used in blues).

Fig. 29

We thus have two tensions of M3 and two tonal vectors separated by a distance of m3. Tonal vectors that acquire more force if they become 7M3 structures.

See also 6.2.5.

3.1.7 Cluster chords

They are chords of genre C^B (o C^D¬).

It is the most dissonant chord family since the two functional fundamentals (the two M3) are separated by an interval of m2.

Figure 30 shows some chords of this family. Note that if we complete the triads of C and/or B, we add tensions that appear in other families. If we put the note G, we add a new tension of M3 (+G^B, then it also acquires the augmented chord character) and if F{ appears, we add a new tritone tension (+\D^C). I use the word «gene» which I believe it works to exemplify this fact: they have «genes» from other families. In the same way that the diminished seventh chord has genes from the dominant chord families and the symmetrical chord families, or chord ~C⁷_Ã has genes from the major-minor family and the dominant family, cluster chords soon

acquire genes from other families when the convergent structures of C and B are completed.

Fig. 30

In the symbology we put B above because it is the harmonic 5f of 3f of C, but we could also put it below (B^C) as main fundamental since, as we will see, the chord better resolves on a chord based on E (B|E) than on one based in F (C|F) (see 6.2.5).

With the chord families studied so far we have all possible combinations between two functional fundamentals.

3.1.8 Suspended chords

They are chords that do not have functional tensions. That is to say, they do not have intervals of M3 nor intervals of tritone. They are basically quartal and quintal chords. Therefore in their symblogy no capital letters appear (they have no functional fundamentals). In jazz theory are represented as C^sus2 or C^sus4 although our family has a wider range.

They are chords of genre c⁽⁷⁾, c_a, c^g o d^c (c^b¬) (in lowercase). Some of them, according to the note they have in the bass, can be coded in two different ways (c^~g or d^~c).

We have represented some of them in figure 31.

Fig. 31

I use the term "suspended" not as a synonym of nonchord suspension tone (ritardo in italian, although some of these chords may be considered with suspensions in certain harmonic progressions), but because they do not have harmonic tension (although can have sonance tension) and therefore we could say that they are like

«suspended» in the air. Most are not very consonant, but have almost no tonal tension. See also 6.2.5.

3.1.9 Other chords

Most three- and four-note chords can be included in any of these families we have seen so far, as well as pretty five- and six-note chords. From five notes many chords enjoy the properties of two or more families at a time (see annex 1). In 3.3 we can see a correspondence of the most used and known chords with their fundamental symbology (and therefore seeing the family to which they belong) that informs us of their internal harmonic tensions.

We have already seen that in these families there are chords, such as the diminished seventh, that have genes from several of them, even an independent family could have been made only for this chord. Also, for example, all chords that include the 7M3 structure (real or virtual) have genes from the dominant chords families. What is really useful and important is to know what are the functional fundamentals of chords and with this information know what types of tensions occur between them, since, looking at the fundamentals of the contiguous chords, we know their global tensions and their homotonic (local) and tonal relaxions or resolutions. As we will see in detail in chapters 6 and 7.

3.2 The functionality of chord families

We can summarize the chord families we have just seen, those that have one or two functional fundamentals (all of them except except the suspended family) using the circle of fifths (figure 32).

Fig. 32

If we add notes to these chords in a way that does not create new functional fundamentals, then this does not affect its harmonic tension (although it can affect the sonance tension). For example, adding note A to chords C or C^G to convert them into chords of the minor chord family. As I said I have preferred, however, to put the major and minor chords into two distinct families (they could have been placed into one) because of their characteristic sonority and the great literature that exists in the history of music about the chords with the major third and those who have the minor third. They have a different sonority, but their harmonic function, in the sense of the notes to which they want to resolve homotonically (locally, independently of the tonality), is similar (determined by the M3 intervals they contain). As we have already seen, proof of this is the functional symbology applied by Riemann to minor chords (see 1.8 and 5.3) or the use of Rameau's sixte ajoutée or the use of C⁶ or C½ symbols for chords in which A is added to the major triad and, in both cases, maintain the function of C (as long as the bass is C).

Another added note that usually does not vary the function of a chord is the major second major of the fundamental (D for chords with fundamental C —the fifth of his fifth).

In any harmonization, if chords are changed by other chords of the same family (having the same functional fundamentals), the color and con(sonance) of the harmonization vary, but its functional structure remains similar. Or, in other words, if we want to color chords without varying their harmonic function, we can add or change notes as long as we do not create new uppercase fundamentals (functional fundamentals) in the functional symbols.

In Example 3.1 we have two cadential progressions. In (a) a simple version is exposed and in (b) the chords are colored by changing or adding notes, which do not substantially modify the functional structure of the chords. C is converted to C^G_f{ (it would also be possible to code it as ~C^b), C^G comes from the major chord family of C and the added F{ creates a tritone (CF{) tension, but since there are no notes A or E¬ in the chord the virtual fundamentals that are created (\D y \A¬) are very weak. F_d becomes F_d^C, of the same family of minor chords. Gµ becomes G⁷⁹, of the same family of dominant chords. The final triad C becomes C_a^G. C^G is from the family of C and the added A gives us another example of what we have discussed above regarding the true functional fundamental of the minor chord. In fact this last chord is not heard as an enriched inversion of A minor but, being C in the bass and having the added note D, A is felt like a Pythagorean harmonic of C (C:G:D:A).

Ex. 3-1 (Listen on youtube)

Example (b) is a re-harmonization of (a) using chords from the same family or maintaining the functional fundamentals of the four chords, but a more aggressive harmonization could have been done, adding new functional fundamentals without necessarily losing the cadential sense of the progression. We should only be careful not to lose the 7M3 structure (of C major) in the two chords prior to the final chord (although in certain cases the 7M3 structure of this tone could be shared with other 7M3 structures).

3.3 Correspondence between the main known chords and the fundamental symbology
It will help to clarify the meaning of chord families and the fundamental symbology if we draw a correspondence between the main chords known in the history of music and the fundamental symbols according to the harmonic theory of this book.

In figure 33, below each chord, we place in the first line our fundamental symbology and, below, other commonly used symbols, although the symbology to represent chords are not currently standardized. For the case of augmented sixth chords see figure 6.

Figure 34 shows the fundamental symbology of known chords that have been baptized with a name. We put the symbols independently of the tonal context in which the chords are immersed. For example, the Tristan chord, if it is isolated (without tonal context) creates a clear tonal vector towards F{; if the chord were to be resolved in this tonic, the F should be enharmonized to E{, leading-tone of the tonality. But in Wagner's work the F acts as Phrygian dominant (upper leading-tone) of E⁷ (see example 7-26).

Fig. 33

Fig. 34

3.4 Chord inversions and their optional symbology

We have already seen in 2.3 the strength of the octaves and deduced the functional equality between inversions. Whatever the inversion, the notes of the chord, as harmonics, are repeated in their upper octaves. This causes that, regardless of the bass of the chord, the ratios between intervals remain the same and by the virtual fundamental effect the ear functionally matches the chords and assigns them the same fundamental(s). In figure 16 we set as example the inversions of the major triad, but could be any other chord.
In general, the harmonic function of a chord changes little if you change the order of notes, including the bass.

Due to the significant power of harmonic 3f (fifth) there are cases where (changing bass) we are close to the boundary of the functional change (as we have seen in 2.3), as would be the case of the cadential æ chord where, in a tonal diatonic context, the upper notes can also be heard as appoggiaturas notes with a tendency to «resolve» in the harmonics 3f and 5f of the bass. In fact, it is not a question of discussing whether it is one thing or another but, as so often happens in harmonic analysis, be aware that both facts are perceived simultaneously.

Minor chords can be separated in two fundamentals, this explains the different functional consideration that has been given to this chord —already since Rameu times— according to the note that is in the bass. As we have seen, the chord ACE

can be considered an A minor chord or a C (major) chord with the sixte ajoutée if C is on the bass. In jazz, in order to symbolize the chord CEGA the C⁶ symbol is used when C is on the bass and is functionally used as a C major chord, even as final chord. Our symbol C_a reflects this duality of the A minor chord with that of C major sixth.

Therefore, having a note or another in the bass may have its importance, especially with respect to sonance, but in some cases may also vary the function of the chord.

This is why in the analyzes of works where the chords are not very complex a special symbology might be used to differentiate the inversions, but for many other analyzes, in which one only needs to get an idea of the harmonic functional progressions, it will not be necessary to differentiate between inversions. In fact, in most examples of chapter 7 this symbology is not used.

We will next do a proposal of symbology that differentiates inversions in case one wants to incorporate it to the analysis or to do a harmonic scheme of a score without the notes.

Our fundamental symbology already incorporates all the information of the notes and is independent of the musical scales, so it is not necessary to add numbers (other than 7 and 9) on the bass to specify the rest of the notes, as is done with the baroque figured bass. In jazz theory inversions are usually specified by placing a slash after the chord symbol and adding the bass note if it does not match with the chord root. For example, the 3rd inversion of the dominant seventh chord with root C is symbolized C⁷/B¬ (B¬ in the bass).

With our intention of seeking simplicity in symbols that at first sight may seem complex and because, if we are doing the analysis with the score, the bass note is easily localizable, we will only indicate if the chord is an inversion or not. To do this we will simply put a line under the symbol in case the chord is not in the fundamental state (or does not have the main fundamental on the bass). Looking at the bass in the score we will know quickly which inversion is involved. We have already used this method in figure 6, and in figure 35 we give some more examples. We will always consider that a chord is in a fundamental state when the bass of the chord coincides with the fundamental that is in the lower position in the symbols, even it is in lowercase.

If we have a virtual fundamental, the fundamental does not exist in the chord, in these cases we can consider fundamental state the chord with the M3 of the virtual fundamental in the bass, which is the most stable position since we have m3 and tritone of the bass above (the structure of the harmonics of a virtual fundamental). The symmetrical chords should be coded according to a correct tonal context.

Fig. 35

As we have said, if music or chords have some complexity, it is not necessary to indicate the inversions if we want only to get an idea of the harmonic tensions that are at stake. For very paradigmatic cadences in musical theory, such as the cadential æ (the tonic chord with the dominant in the bass), we will use the symbol Dæ in the tonal analysis (D of dominant).

If our symbology is used to harmonize melodies (without drawing complete chord notes), then we can specify, as in jazz/modern music, the bass note below the line (when the chord is not in the fundamental state).

As for pedals points, we will represent them by placing the pedal note with a line that will cover its entire duration, below the rest of the symbols representing the rest of the notes. See examples 7-7, 7-9, 7-16, 7-21 or 7-25 of chapter 7.

Chapter 4