Sabadell, 24 de maig de 1995

Admirado profesor Murray Gell-Mann,

He leído su libro El quark y el jaguar y me ha gustado muchísimo. Yo soy compositor, aunque he tenido una educación científica y sigo todos los progresos científicos con mucho interés y atención.

La síntesis sobre el mundo de las partículas elementales la he encontrado especialmente genial y clarísima. Es el primer libro coherente que he leído que establece las bases de la difícil relación entre macrocosmos y microcosmos. He encontrado en su libro un espíritu de sinceridad y autenticidad inhabitual en urgar en el fondo de las cosas dejando de lado prejuicios y no dejándose influenciar por ideas establecidas.

Sin embargo hay algunos puntos que no me han quedado claros, uno de ellos es la relación entre entropía y complejidad. ¿Es el aumento de la complejidad una manifestación del aumento de entropía? ¿Aumenta la complejidad a costa de la energía de otros sistemas? ¿Puede disminuir la complejidad en sistemas cerrados?

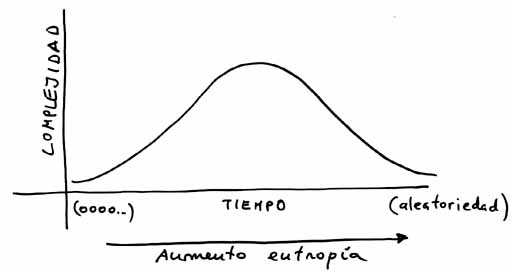
¿Podría formar la complejidad algo parecido a una campana de Gauss? La naturaleza parece darnos, dentro de la entropía creciente, muchos ejemplos de este tipo:

- El nacimiento, crecimiento, decaimiento y muerte de civilizaciones.

- El nacimiento, crecimiento, decaimiento y muerte de organismos vivos.

- El nacimiento, crecimiento, decaimiento y muerte de ciclones

- El nacimiento, crecimiento, decaimiento y muerte de estrellas y planetas.

- El nacimiento, crecimiento, decaimiento y muerte de las empresas

etc.

Y, en definitiva, el nacimiento, crecimiento, decaimiento y muerte del universo (¿renacimiento si hay suficiente masa?)

Parece un panorama sombrío y pesimista, pero no lo es, porque aparecen nuevas civilizaciones, nuevos organismos, nuevos ciclones, nuevas estrellas, nuevas empresas y, nuevos universos (?).

En los dos extremos de la curva de Gauss habría la mínima complejidad (una cadena de bits 0 en un extremo y la completa aleatoriedad en el otro, tal como usted explica en la pag. 77 de su libro, aunque no aparece la variable tiempo). Estas curvas de complejidad estarían incluidas unas dentro de las otras, a modo de geometría fractal.

Aprovechando su sugerencia del capítulo 17 (Del aprendizaje al pensamiento creativo) le explico, desde mis modestos conocimientos, algunos pensamientos disparatados:

Cuando era adolescente me interesaba mucho el tema de los OVNIS (UFO en inglés). Leía en revistas que las supuestas naves inflingían las leyes de la física porque hacían trayectorias en ángulo recto de 90º a grandes velocidades. Yo, con mi mano cogía un pequeño avión de juguete y me preguntaba: ¿Por qué es imposible?, yo lo hago con el avión que tengo en mis manos. Cogía el pequeño avión de plástico con mi mano derecha y realizaba una rápida trayectoria en ángulo recto. Aunque ahora se que la causa de la imposibilidad son las distintas escalas de espacio y masa, siempre me ha quedado la intuición de que este razonamiento, que hacía en mi juventud, tiene algo de verdadero. En todo caso, esto implica que las leyes de la física dependen de la escala. (¿es la velocidad de la luz la que fija la escala, o a la inversa? ¿queda determinada la escala por partículas elementales o supercuerdas?)

Otra idea descabellada es que cuando estudiaba matemáticas en la universidad llegábamos a los números reales a través de la convergencia de sucesiones de Cauchy de números racionales. Una vez establecidos los números reales podíamos trabajar con integrales, ecuaciones diferenciales, etc... Pero, en el mundo real, ¿podemos formar sucesiones de Cauchy con las variables tiempo y espacio? No, a causa de los paquetes mínimos de Planck (en contra de la paradoja de Zenon, en la naturaleza, entre dos puntos no siempre hay uno en medio). Entonces, ¿es legítimo trabajar con integrales y otros mecanismos matemáticos en el microcosmos?

Otro pensamiento: ¿es razonable afirmar que después de una gran explosión aparezca, al cabo de cierto tiempo, en medio de una curiosa y orgánica polvareda, un libro explicándola? Yo no lo encuentro muy razonable, aunque en el caso de nuestro universo parece ser que es cierto.

Ahora me gustaría hablarle de mi libro, del cual le mando un ejemplar con una traducción provisional al inglés.

No se la relación que puede haber entre los armónicos de los sonidos y los armónicos de las supercuerdas pero me gustaría que diera una ojeada a su curiosa geometría fractal reflejada en la pág.11. También la gran importancia que han tenido para el arte musical los armónicos primos 2, 3 y 5. (pág 13, nota 14).

En la pág. 41 he encontrado la fórmula para determinar el número de acordes según las relaciones de equivalencia N₂, N₃, N₄ y N₅, pero he sido incapaz de encontrarla para N₆, que la he deducido a partir de N₅, ¿podría decirme alguien con conocimientos musicales si existe una fórmula independiente para N₆?

Si usted o algún alumno suyo tiene la amabilidad y la paciencia de contestarme pueden hacerlo perfectamente en inglés.

Gracias por su atención.

Se despide afectuosamente,